《三角函数的概念》三角函数PPT课件(第2课时同角三角函数的基本关系)

《三角函数的概念》三角函数PPT课件(第2课时同角三角函数的基本关系) 第一部分内容：学 习 目 标 1.理解并掌握同角三角函数基本关系式的推导及应用．(重点) 2．会利用同角三角函数的基本关系式进行化简、求值与恒等式证明．(难点) 核 心 素 养 1.通过同角三角函数的基本关系进行运算，培养数学运算素养． 2．借助数学式子的证明，培养逻辑推理素养. ... ... ... 三角函数的概念PPT，第二部分内容：自主预习探新知 新知初探 1．平方关系 (1)公式：sin2α＋cos2α＝_____. (2)语言叙述：同一个角α的正弦、余弦的平方和等于_____. 2．商数关系 (1)公式：sin αcos α＝_____(α≠kπ＋π2，k∈Z)． (2)语言叙述：同一个角α的正弦、余弦的商等于__________． 思考：对任意的角α，sin22α＋cos22α＝1是否成立？ 提示：成立．平方关系中强调的同一个角且是任意的，与角的表达形式无关． 初试身手 1．化简1－sin23π5的结果是(　　) A．cos3π5　B．sin3π5 C．－cos3π5  D．－sin3π5 2．如果α是第二象限的角，下列各式中成立的是(　　) A．tan α＝－sin αcos α B．cos α＝－1－sin2 α C．sin α＝－1－cos2 α D．tan α＝cos αsin α 3．若cos α＝35，且α为第四象限角，则tan α＝________. ... ... ... 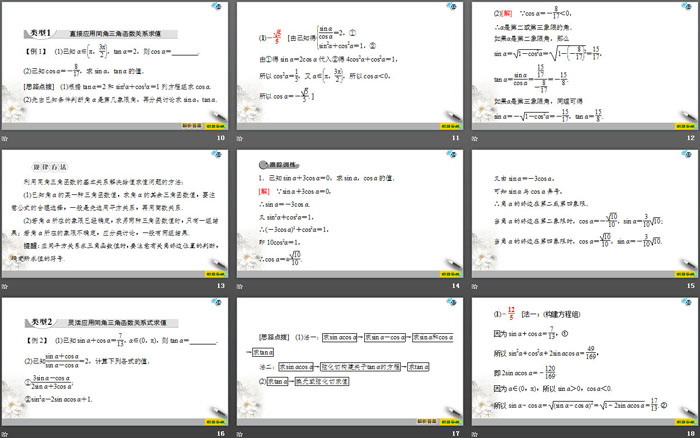三角函数的概念PPT，第三部分内容：合作探究提素养 直接应用同角三角函数关系求值 【例1】(1)已知α∈π，3π2，tan α＝2，则cos α＝________. (2)已知cos α＝－817，求sin α，tan α的值． [思路点拨]　(1)根据tan α＝2和sin2α＋cos2α＝1列方程组求cos α. (2)先由已知条件判断角α是第几象限角，再分类讨论求sin α，tan α. 规律方法 利用同角三角函数的基本关系解决给值求值问题的方法： 1已知角α的某一种三角函数值，求角α的其余三角函数值，要注意公式的合理选择，一般是先选用平方关系，再用商数关系. 2若角α所在的象限已经确定，求另两种三角函数值时，只有一组结果；若角α所在的象限不确定，应分类讨论，一般有两组结果. 提醒：应用平方关系求三角函数值时，要注意有关角终边位置的判断，确定所求值的符号. 跟踪训练 1．已知sin α＋3cos α＝0，求sin α，cos α的值． [解]　∵sin α＋3cos α＝0， ∴sin α＝－3cos α. 又sin2α＋cos2α＝1， ∴(－3cos α)2＋cos2α＝1， 即10cos2α＝1， ∴cos α＝±1010. 又由sin α＝－3cos α， 可知sin α与cos α异号， ∴角α的终边在第二或第四象限． 当角α的终边在第二象限时，cos α＝－1010，sin α＝31010； 当角α的终边在第四象限时，cos α＝1010，sin α＝－31010. 灵活应用同角三角函数关系式求值 【例2】(1)已知sin α＋cos α＝713，α∈(0，π)，则tan α＝________. (2)已知sin α＋cos αsin α－cos α＝2，计算下列各式的值． ①3sin α－cos α2sin α＋3cos α； ②sin2α－2sin αcos α＋1. 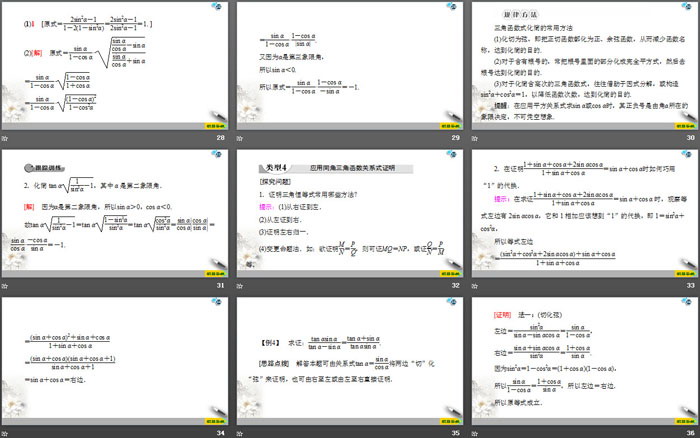[思路点拨](1)法一：求sin αcos α→求sin α－cos α→求sin α和cos α→求tan α 法二：求sin αcos α→弦化切构建关于tan α的方程→求tan α (2)求tan α→换元或弦化切求值 规律方法 1．sin α＋cos α，sin α－cos α，sin αcos α三个式子中，已知其中一个，可以求其他两个，即“知一求二”，它们之间的关系是：(sin α±cos α)2＝1±2sin αcos α. 2．已知tan α＝m，求关于sin α，cos α的齐次式的值 解决这类问题需注意以下两点：(1)一定是关于sin α，cos α的齐次式(或能化为齐次式)的三角函数式；(2)因为cos α≠0，所以可除以cos α，这样可将被求式化为关于tan α的表示式，然后代入tan α＝m的值，从而完成被求式的求值． 提醒：求sin α＋cos α或sin α－cos α的值，要注意根据角的终边位置，利用三角函数线判断它们的符号． ... ... ... 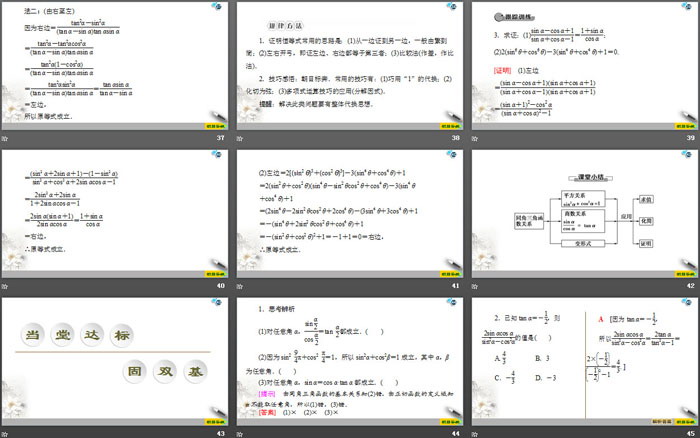三角函数的概念PPT，第四部分内容：当堂达标固双基 1．思考辨析 (1)对任意角α，sin α2cos α2＝tan α2都成立．(　　) (2)因为sin2 94π＋cos2 π4＝1，所以sin2α＋cos2β＝1成立，其中α，β为任意角．(　　) (3)对任意角α，sin α＝cos α•tan α都成立．(　　) [提示]　由同角三角函数的基本关系知(2)错，由正切函数的定义域知α不能取任意角，所以(1)错，(3)错． 2．已知tan α＝－12，则2sin αcos αsin2α－cos2α的值是(　　) A.43　　B．3　　　 C．－43　 D．－3 3．已知α是第二象限角，tan α＝－12，则cos α＝________. ... ... ... 关键词：高中人教A版数学必修一PPT课件免费下载，三角函数的概念PPT下载，三角函数PPT下载，同角三角函数的基本关系PPT下载，.PPT格式；