《向量基本定理与向量的坐标》平面向量初步PPT(平面向量的坐标及其运算)

《向量基本定理与向量的坐标》平面向量初步PPT(平面向量的坐标及其运算) 第一部分内容：课标阐释 1.了解平面向量的正交分解,掌握向量的坐标表示. 2.理解向量坐标的概念,掌握两个向量和、差及数乘向量的坐标运算法则. 3.理解向量的坐标与平面内点的坐标的区别与联系.   ... ... ... 向量基本定理与向量的坐标PPT，第二部分内容：课前篇自主预习 一、平面向量的坐标 1.填空. (1)垂直向量:平面上两个非零向量a与b,如果它们所在的直线互相垂直,我们就称向量a与b垂直,记作a⊥b.规定零向量与任意向量都垂直. (2)正交分解:如果平面向量的基底{e1,e2}中,e1⊥e2,就称这组基底为正交基底;在正交基底下向量的分解称为向量的正交分解. (3)向量的坐标 一般地,给定平面内两个互相垂直的单位向量e1,e2,对于平面内的向量a,如果a=xe1+ye2,则称(x,y)为向量a的坐标,记作a=(x,y). 2.点的坐标与向量的坐标有何区别? 提示:(1)向量坐标与点的坐标有区别,当且仅当向量的起点为坐标原点时,向量坐标才与其终点的坐标相等.如:点A的位置向量(OA) 的坐标(x,y),也就是点A的坐标(x,y);反之,点A的坐标(x,y)也是点A相对于坐标原点的位置向量(OA) 的坐标; (2)符号(x,y)在直角坐标系中有双重意义,它既可以表示一个固定的点,又可以表示一个向量,为了加以区分,在叙述中,就常说点(x,y),或向量(x,y). (3)给定一个向量,它的坐标是唯一的,给定一对实数,由于向量可以平移,以这对实数为坐标的向量有无穷多个. (4)两个向量相等,当且仅当它们的坐标相同. 二、平面上向量的运算与坐标的关系 1.填空. (1)向量加法与减法运算 设a=(x1,y1),b=(x2,y2),则 ①ua+vb=(ux1+vx2,uy1+vy2);②ua-vb=(ux1-vx2,uy1-vy2). (3)平面直角坐标系内两点之间的距离公式与中点坐标公式 设A(x1,y1),B(x2,y2)为平面直角坐标系中的两点,则 (4)向量平行的坐标表示 设a=(x1,y1),b=(x2,y2),则a∥b⇔x2y1=x1y2. 2.做一做:已知向量a=(8,1/2 x) ,b=(x,1),其中x>0,若(a-2b)∥(2a+b),则x的值为(　　) A.4 B.8 C.0 D.2 答案:A ... ... ... 向量基本定理与向量的坐标PPT，第三部分内容：课堂篇探究学习 平面向量的坐标表示 例1如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°, (OA) =a,(AB) =b.四边形OABC为平行四边形.求: (1)向量a,b的坐标; (2)向量(BA) 的坐标; (3)点B的坐标. 求向量的模 例2设平面向量a=(1,2),b=(-2,y),若a∥b,则|2a-b|等于(　　) A.4 B.5 C.3√5 D.4√5 分析:综合应用向量共线的坐标表示和向量模的坐标表示求解. 答案:D 解析:由y+4=0知 y=-4,b=(-2,-4), ∴2a-b=(4,8),∴|2a-b|=4√5 .故选D. 反思感悟求向量的模的两种基本策略 (1)字母表示下的运算: 利用|a|2=a2,将向量模的运算转化为向量与向量的数量积的问题. (2)坐标表示下的运算: 若a=(x,y),则a•a=a2=|a|2=x2+y2,于是有|a|=√(x^2+y^2 ). ... ... ... 向量基本定理与向量的坐标PPT，第四部分内容：思维辨析 共线向量问题——数学方法 典例已知a=(1,2),b=(-3,2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向? 分析:法一:可利用b与非零向量a共线等价于b=λa(λ>0,b与a同向;λ<0,b与a反向)求解; 法二:可先利用坐标形式的等价条件求k,再利用b=λa判定同向还是反向. 解:法一:(共线向量定理法)ka+b=k(1,2)+(-3,2)=(k-3,2k+2), a-3b=(1,2)-3(-3,2)=(10,-4), 当ka+b与a-3b平行时,存在唯一实数λ, 使ka+b=λ(a-3b). 由(k-3,2k+2)=λ(10,-4), ... ... ... 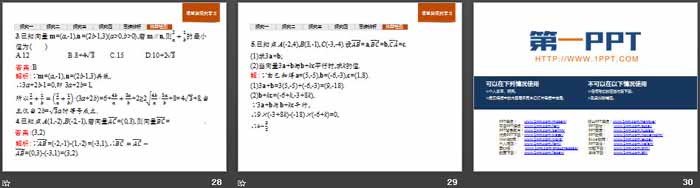向量基本定理与向量的坐标PPT，第五部分内容：当堂检测 1.已知M(3,-2),N(-5,-1),若(MP) ⃗=1/2 (MN) ⃗,则P点的坐标为(　　) A.(-8,1) B.(8,-1) C.(- 1,- 3/2)  D.(1,  3/2) 2.已知a=(4,2),b=(x,6),且a∥b,则x=(　　) A.12 B.13 C.14 D.15 答案:A 解析:a=(4,2),b=(x,6),且a∥b, 则x1y2=x2y1即2x=24⇒x=12. 故选A. ... ... ... 关键词：高中人教B版数学必修二PPT课件免费下载，向量基本定理与向量的坐标PPT下载，平面向量初步PPT下载，平面向量的坐标及其运算PPT下载，.PPT格式；