人教A版(2019)数学必修第二册《概率》统计与概率PPT(随机事件的独立性)
展开
《概率》统计与概率PPT(随机事件的独立性)
第一部分内容:课标阐释
1.在具体情境中,了解两个事件相互独立的概念.
2.能利用相互独立事件同时发生的概率公式解决一些简单的实际问题.
3.综合运用互斥事件的概率加法公式及独立事件的乘法公式解决一些问题.
4.通过实际问题的解决提高数学建模及数据处理能力.
... ... ...
概率PPT,第二部分内容:课前篇自主预习
一、相互独立事件的定义和性质
1.填空.
(1)定义:一般地,当P(AB)=P(A)P(B)时,就称事件A与B相互独立(简称独立).事件A与B相互独立的直观理解是,事件A是否发生不会影响事件B发生的概率,事件B是否发生也不会影响事件A发生的概率.
(2)性质:如果事件A与B相互独立,则¯A与B,A与¯B,¯A 与¯B也相互独立.
2.互斥事件与相互独立事件有何区别?
二、独立事件的概率公式
1.填空.
(1)若事件A,B相互独立,则P(AB)=P(A)P(B);
(2)若事件A1,A2,…,An相互独立,则P(A1A2…An)=P(A1)P(A2)…P(An).
2.做一做:在某道路A,B,C三处设有相互独立工作的交通灯,这三盏灯在一分钟内开放绿灯的概率分别为__________.某辆车在这条道路上匀速行驶,则三处都不停车的概率为__________.
... ... ...
概率PPT,第三部分内容:课堂篇探究学习
相互独立事件的判断
例1判断下列各对事件是不是相互独立事件.
(1)甲组有3名男生、2名女生;乙组有2名男生、3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,“从甲组中选出1名男生”与“从乙组中选出1名女生”;
(2)容器内盛有5个白乒乓球和3个黄乒乓球,“从8个球中任意取出1个,取出的是白球”与“从剩下的7个球中任意取出1个,取出的还是白球”;
(3)掷一枚骰子一次,“出现偶数点”与“出现3点或6点”.
点拨(1)利用独立概念的直观解释进行判断.(2)计算事件“从8个球中任意取出1个,取出的是白球”与事件“从剩下的7个球中任意取出1个,取出的还是白球”的概率是否相同进行判断.(3)利用事件独立的定义判断.
解:(1)“从甲组中选出1名男生”这一事件是否发生,对“从乙组中选出1名女生”这一事件发生的概率没有影响,所以它们是相互独立事件.
(2)“从8个球中任意取出1个,取出的是白球”的概率为5/8,若这一事件发生了,则“从剩下的7个球中任意取出1个,取出的仍是白球”的概率为4/7;若前一事件没有发生,则后一事件发生的概率为5/7,可见,前一事件是否发生,对后一事件发生的概率有影响,所以二者不是相互独立事件.
(3)记A:出现偶数点,B:出现3点或6点,则A={2,4,6},B={3,6},AB={6},
所以P(A)=3/6=1/2,P(B)=2/6=1/3,P(AB)=1/6.
所以P(AB)=P(A)P(B),
所以事件A与B相互独立.
反思感悟判断事件是否相互独立的方法
(1)定义法:事件A,B相互独立⇔P(AB)=P(A)P(B).
(2)直接法:由事件本身的性质直接判定两个事件发生是否相互影响.
变式训练(1)下列事件中,A,B是相互独立事件的是( )
A.一枚硬币掷两次,A=“第一次为正面”,B=“第二次为反面”
B.袋中有2白,2黑的小球,不放回地摸两球,A=“第一次摸到白球”,B=“第二次摸到白球”
C.掷一枚骰子,A=“出现点数为奇数”,B=“出现点数为偶数”
D.A=“人能活到20岁”,B=“人能活到50岁”
(2)甲、乙两名射手同时向一目标射击,设事件A:“甲击中目标”,事件B:“乙击中目标”,则事件A与事件B ( )
A.相互独立但不互斥 B.互斥但不相互独立
C.相互独立且互斥 D.既不相互独立也不互斥
答案:(1)A (2)A
解析:(1)A中,把一枚硬币掷两次,对于每次而言是相互独立的,其结果不受先后影响,故A与B相互独立;B中,是不放回地摸球,显然事件A与B不相互独立;C中,事件A,B为互斥事件,不相互独立;D中,事件B发生的概率受事件A是否发生的影响.故选A.
(2)向同一目标射击,甲、乙两射手是否击中目标是互不影响的,所以事件A与B相互独立;向同一目标射击,甲、乙两射手可能同时击中目标,也就是说事件A与B可能同时发生,所以事件A与B不是互斥事件.故选A.
... ... ...
概率PPT,第四部分内容:思维辨析
事件的相互独立性与互斥性——数学方法
典例小王某天乘火车从重庆到上海去办事,若当天从重庆到上海的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响.求:
(1)这三列火车恰好有两列正点到达的概率.
(2)这三列火车至少有一列正点到达的概率.
分析:(1)这三列火车之间是否正点到达互不影响,因此本题是相互独立事件同时发生的概率问题,注意两列正点到达所包含的情况.
(2)这三列火车至少有一列正点到达的对立事件是三列火车都没正点到达,这种情况比正面列举简单些,因此利用对立事件的概率公式求解.
方法点睛与相互独立事件有关的概率问题求解策略
明确事件中的“至少有一个发生”“至多有一个发生”“恰好有一个发生”“都发生”“都不发生”“不都发生”等词语的意义.
一般地,已知两个事件A,B,它们的概率分别为P(A),P(B).
(1)A,B中至少有一个发生为事件A+B.
(2)A,B都发生为事件AB.
... ... ...
概率PPT,第五部分内容:当堂检测
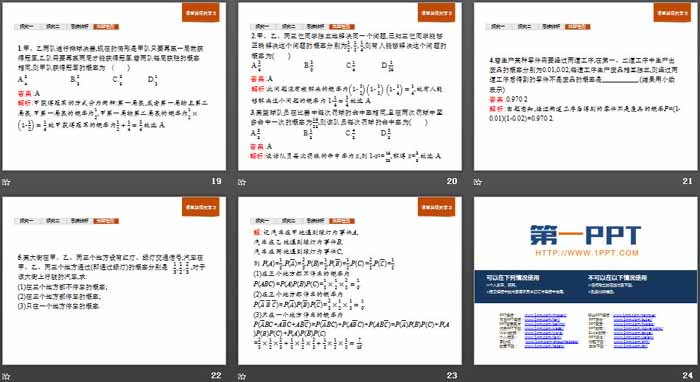
1.甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获得冠军,乙队需要再赢两局才能获得冠军.若两队每局获胜的概率相同,则甲队获得冠军的概率为 ( )
A.3/4 B.2/3 C.3/5 D.1/2
2.甲、乙、丙三位同学独立地解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为1/2,1/3,1/4,则有人能够解决这个问题的概率为( )
A.3/4 B.3/8 C.1/4 D.1/24
3.某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为16/25,则该队员每次罚球的命中率为( )
A.3/5 B.1/5 C.4/5 D.2/5
4.若生产某种零件需要经过两道工序,在第一、二道工序中生产出废品的概率分别为0.01,0.02,每道工序生产废品相互独立,则经过两道工序后得到的零件不是废品的概率是_______.(结果用小数表示)
答案:0.970 2
解析:由题意知,经过两道工序后得到的零件不是废品的概率P=(1-0.01)(1-0.02)=0.970 2.
... ... ...
关键词:高中人教B版数学必修二PPT课件免费下载,概率PPT下载,统计与概率PPT下载,随机事件的独立性PPT下载,.PPT格式;