人教A版(2019)数学必修第一册《周期性、奇偶性》三角函数PPT
展开
《周期性、奇偶性》三角函数PPT
第一部分内容:课标阐释
1.通过具体问题了解周期函数的概念,并能举出一些具有周期现象的实例.
2.理解正弦函数与余弦函数的周期性,会求函数的周期.
3.理解三角函数的奇偶性以及对称性,会判断给定函数的奇偶性.
... ... ...
周期性奇偶性PPT,第二部分内容:自主预习
一、周期函数
1.由正弦函数的图象可知,正弦曲线每相隔2π个单位重复出现,这一规律的理论依据是什么?设f(x)=sin x,则sin(x+2kπ)=sin x(k∈Z)可以怎样表示?
提示:sin(x+2kπ)=sin x(k∈Z);f(x+2kπ)=f(x).
2.填空
周期函数的定义:对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数y=f(x)叫做周期函数,非零常数T叫做这个函数的周期.
3.周期函数的周期是否唯一?正弦函数的周期有哪些?是否存在最小的一个?是否存在一个最小的正的周期?
提示:周期函数的周期不唯一;正弦函数的周期为2kπ(k∈Z,k≠0);不存在最小的一个;存在一个最小的正的周期2π.
4.填空
最小正周期:如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期.在没有特殊说明的情况下,三角函数的周期均是指它的最小正周期.
5.做一做
(1)若函数f(x)满足f(x+3)-f(x)=0,则函数f(x)是周期为_________的周期函数.
(2)若函数f(x)的最小正周期是4,则必有f(x+8)________f(x)(填“=”或“≠”).
解析:(1)由已知得f(x+3)=f(x),所以f(x)是周期为3的周期函数.
(2)由已知得f(x+8)=f(x+4)=f(x).
答案:(1)3 (2)=
二、正弦函数与余弦函数的周期性
1.就周期性而言,对正弦函数有什么结论?对余弦函数呢?
提示:正弦函数是周期函数,最小正周期是2π;余弦函数也是周期函数,最小正周期也是2π.
2.填空
(1)正弦函数y=sin x是周期函数,2kπ(k∈Z,且k≠0)都是它的周期,最小正周期是2π.
(2)余弦函数y=cos x是周期函数,2kπ(k∈Z,且k≠0)都是它的周期,最小正周期是2π.
... ... ...
周期性奇偶性PPT,第三部分内容:探究学习
求三角函数的周期
例1求下列三角函数的周期:
(1)y=3sin x,x∈R;
(2)y=cos 2x,x∈R;
(3)y=sin(1/3 x"-" π/4),x∈R;
(4)y=|cos x|,x∈R.
分析:对于(1)(2)(3),可用公式法求周期;对于(4),可借助函数图象观察求得周期.
解:(1)3sin(x+2π)=3sin x,由周期函数的定义知,y=3sin x的周期为2π.
(2)cos 2(x+π)=cos(2x+2π)=cos 2x,由周期函数的定义知,y=cos 2x的周期为π.
(3)sin[1/3 "(" x+6π")-" π/4]=sin(1/3 x+2π"-" π/4)=sin(1/3 x"-" π/4),由周期函数的定义知,y=sin(1/3 x"-" π/4)的周期为6π.
(4)y=|cos x|的图象如图(实线部分)所示,
由图象可知,y=|cos x|的周期为π.
反思感悟 求函数最小正周期的常用方法
求三角函数的周期,一般有两种方法:(1)公式法,即先将函数化为y=Asin(ωx+φ)+B或y=Acos(ωx+φ)+B的形式,再利用T=2π/("|" ω"|" )求得;(2)图象法,利用变换的方法或作出函数的图象,通过观察得到最小正周期.
三角函数奇偶性及其应用
例2判断下列函数的奇偶性:
(1)f(x)=|sin x|+cos x;
(2)f(x)=sin(3x/4+3π/2);
(3)f(x)=(1+sinx"-" cos^2 x)/(1+sinx).
分析:求定义域→判断定义域是否关于原点对称→看f(-x)与f(x)的关系→确定奇偶性
... ... ...
周期性奇偶性PPT,第四部分内容:思维辨析
对周期函数的概念理解不清致误
典例 下列说法中,正确的有________.(填序号)
①函数f(x)=sin(2x+π/3),x∈[-π,π]是周期函数;
②函数f(x)=sin|x|,x∈R是周期函数;
③函数y=|sin(x+π/2)|的最小正周期为π;
④若函数y=2sin(ωx+π/6)的最小正周期为4π,则ω=1/2.
错解①②③④
本题错在什么地方?你能发现吗?怎样避免这类错误呢?
提示:根据周期函数的定义、三角函数的图象以及三角函数周期公式对各个命题加以判断.
正解:对于①,由于函数定义域为[-π,π],故函数不是周期函数,该命题错误;对于②,画出函数y=sin|x|的图象,由图象可知,函数不是周期函数,该命题错误;对于③,y=|sin(x+π/2)|=|cos x|,由图象可知函数周期为π,该命题正确;对于④,依题意应有2π/("|" ω"|" )=4π,故ω=±1/2,该命题错误.
答案:③
防范措施 研究三角函数的周期时,注意从函数的定义域、解析式以及图象等多方面进行分析,如果通过公式不易求出函数周期,可以通过观察函数图象来确定函数的周期,特别是含有绝对值符号的函数.
... ... ...
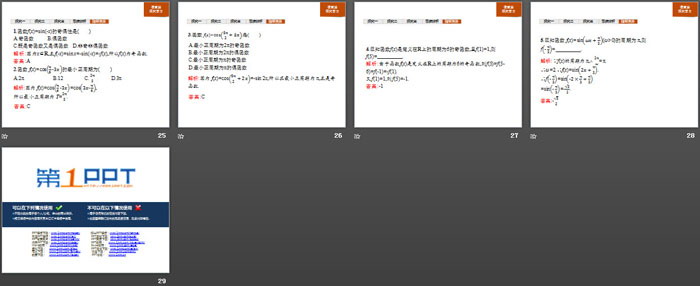
周期性奇偶性PPT,第五部分内容:随堂演练
1.函数f(x)=sin(-x)的奇偶性是( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.非奇非偶函数
解析:因为x∈R,且f(-x)=sin x=-sin(-x)=-f(x),所以f(x)为奇函数.
答案:A
2.函数f(x)=cos(π/6 "-" 3x)的最小正周期为( )
A.2π B.12 C.2π/3 D.3π
解析:因为f(x)=cos(π/6 "-" 3x)=cos(3x"-" π/6),
所以最小正周期为T=2π/3.
答案:C
... ... ...
关键词:高中人教A版数学必修一PPT课件免费下载,周期性奇偶性PPT下载,三角函数PPT下载,.PPT格式;