《指数》指数函数与对数函数PPT课件

《指数》指数函数与对数函数PPT课件 第一部分内容：学习目标 理解n次方根和根式的概念，掌握根式的性质，会进行简单的求n次方根的运算 理解整数指数幂和分数指数幂的意义，并能熟练掌握根式与分数指数幂之间的相互转化 理解指数幂的含义及其运算性质 会根据已知条件，利用指数幂的运算性质、根式的性质进行相关求值运算 ... ... ... 指数PPT，第二部分内容：自主学习 问题导学 预习教材P104－P109，并思考以下问题： 1．n次方根是怎样定义的？ 2．根式的定义是什么？它有哪些性质？ 3．有理数指数幂的含义是什么？怎样理解分数指数幂？ 4．有理指数幂有哪些运算性质？ 新知初探 1．n次方根 ■名师点拨 0的任何次方根都是0，即n0＝0. 2．根式 (1)定义：式子_____叫做根式，这里n叫做__________，a叫做__________． (2)性质：(n＞1，且n∈N*) ①(na)n＝_____． ②nan＝____，n为奇数， _____，n为偶数. ■名师点拨 nan与(na)n的区别 (1)nan是实数an的n次方根，是一个恒有意义的式子，不受n的奇偶限制，但这个式子的值受n的奇偶限制． (2)(na)n是实数a的n次方根的n次幂，其中实数a的取值由n的奇偶决定．其算法是对a先开方，后乘方(都是n次)，结果恒等于a. 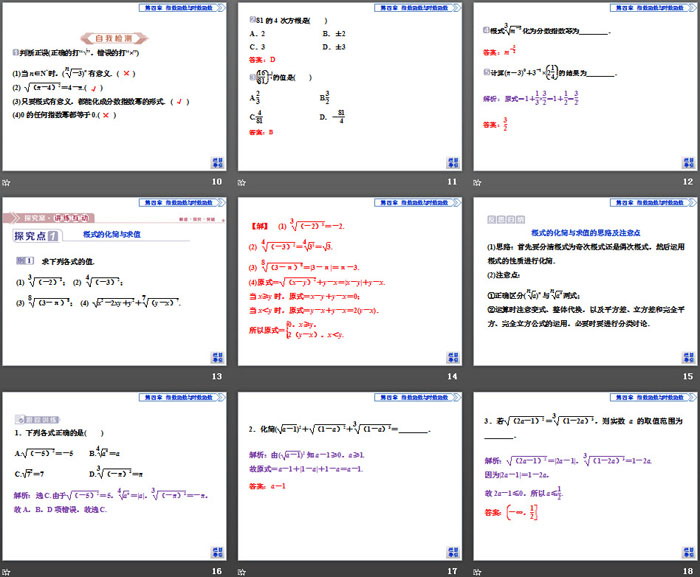3．分数指数幂的意义 ■名师点拨 分数指数幂amn不可以理解为mn个a相乘． 4．指数幂的运算性质 (1)aras＝_____ (a＞0，r，s∈R)． (2)(ar)s＝_____ (a＞0，r，s∈R)． (3)(ab)r＝_____ (a＞0，b＞0，r∈R)． 自我检测 判断正误(正确的打“√”，错误的打“×”) (1)当n∈N*时，(n－3)n有意义．(　　) (2)（π－4）2＝4－π.(　　) (3)只要根式有意义，都能化成分数指数幂的形式．(　　) (4)0的任何指数幂都等于0.(　　)  81的4次方根是(　　) A．2  B．±2 C．3  D．±3 ... ... ... 指数PPT，第三部分内容：讲练互动 根式的化简与求值 求下列各式的值． (1) 3（－2）3； (2) 4（－3）2； (3) 8（3－π）8； (4) x2－2xy＋y2＋7（y－x）7. 反思归纳 根式的化简与求值的思路及注意点 (1)思路：首先要分清根式为奇次根式还是偶次根式，然后运用根式的性质进行化简． (2)注意点： ①正确区分(na)n与nan两式； ②运算时注意变式、整体代换，以及平方差、立方差和完全平方、完全立方公式的运用，必要时要进行分类讨论．　 跟踪训练 1．下列关系式中，根式与分数指数幂的互化正确的是________(只填序号)． ①－x＝(－x)12(x＞0)； ②6y2＝y13(y＜0)； ③x－34＝41x3(x＞0)； ④x－13＝－3x(x≠0)． 2．用分数指数幂的形式表示下列各式(a>0，b>0)： (1)a2a；(2)3a2•a3；(3)(3a)2•ab3；(4)a26a5. 利用指数幂的性质化简求值 计算下列各式(式中字母都是正数)： (1)2350＋2－2×214－12－(0.01)0.5； (2)2790.5＋0.1－2＋21027－23－3π0＋3748； (3)(a－2b－3)•(－4a－1b)÷(12a－4b－2c)； (4)23a2÷46a•b•3b3. 规律方法 利用指数幂的运算性质化简求值的方法 (1)进行指数幂的运算时，一般化负指数为正指数，化根式为分数指数幂，化小数为分数，同时兼顾运算的顺序． (2)在明确根指数的奇偶(或具体次数)时，若能明确被开方数的符号，则可以对根式进行化简运算． (3)对于含有字母的化简求值的结果，一般用分数指数幂的形式表示．　 ... ... ... 指数PPT，第四部分内容：达标规划 1．将532写成根式的形式，正确的是(　　) A.352　　B.35 C．532      D.53 2．计算4（－5）4的结果是(　　) A．5 B．－5 C．±5 D．不确定 3．若a<14，则化简（4a－1）2的结果是(　　) A．4a－1  B．1－4a C．－4a－1  D．－1－4a ... ... ... 关键词：高中人教A版数学必修一PPT课件免费下载，指数PPT下载，指数函数与对数函数PPT下载，.PPT格式；